Uma figura notável na geometria é o pentágono. É comum que, por vários motivos, precisemos encontrar a área do pentágono.
Obter a área e o perímetro de um pentágono é fácil, mas devemos conhecer algumas características básicas como quantos lados tem um pentágono (cinco), o que é um lado ou um apótema.
O que é um pentágono?
Um pentágono é um polígono com cinco lados e cinco vértices.
Por sua vez, um polígono é uma figura geométrica bidimensional com um número finito de segmentos de reta consecutivos não colineares conectados por suas duas extremidades, ou seja, formando um espaço fechado.
Os pentágonos são a base de alguns corpos geométricos, como o prisma pentagonal ou o dodecaedro.
Tipos de pentágonos
Os pentágonos podem ser classificados em várias categorias, dependendo de sua forma:
-
Pentágono regular: É aquele que tem todos os seus lados e ângulos iguais.
-
Pentágono irregular: Não tem todos os seus lados e ângulos iguais.
-
Pentágono convexo: Todos os ângulos internos são menores que 180°.
-
Pentágono côncavo: Pelo menos um dos ângulos internos é maior que 180°.
-
Pentágono Inscrito: Um pentágono cujos vértices estão todos no mesmo círculo.
-
Pentágono circunscrito: É aquele cuja circunferência é tangente a todos os seus lados.
Características de um pentágono
Abaixo listamos as características mais significativas deste tipo de figuras geométricas planas:
-
Um pentágono é formado por cinco lados e cinco ângulos. Os diferentes tipos de pentágonos são classificados com base em seus lados e ângulos.
-
Todos os cinco ângulos internos somam 540º.
-
Se for regular, todos os ângulos internos medem 108° e, portanto, todos os ângulos externos medem 72°.
-
O ângulo central do pentágono regular 360° / 5 = 72°. O ângulo central é aquele formado por duas linhas retas que unem as duas extremidades de um lado ao centro da figura.
-
É composto por cinco diagonais.
-
De cada vértice podem ser desenhadas duas diagonais para outro vértice.
-
Quando o pentágono é regular, as diagonais em cada vértice formam três ângulos de 36° e dividem o pentágono regular em três triângulos isósceles.
-
O perímetro de um pentágono regular ou irregular é a soma dos comprimentos de todos os seus lados. Se for um polígono regular, é o comprimento de um lado multiplicado por cinco.
Como você pode encontrar a área de um pentágono?
Existem várias maneiras de obter a área de um pentágono regular dependendo dos dados que temos. Uma fórmula para a área desta figura geométrica é:
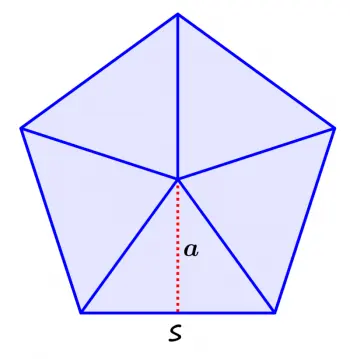
A = (5/2)·c·a
Onde "c" se refere ao comprimento de um lado e "a" se refere ao comprimento do apótema.
Se conhecermos o perímetro: a fórmula se torna A = p·a/2; onde "p" é o perímetro.
Se conhecemos o apótema, podemos usar a fórmula:
A = (5 · (a2)) / (4 · tan(36))
Onde "a" se refere ao apótema da figura.
Calculando a área de um triângulo
A área de um pentágono também pode ser calculada dividindo-a em triângulos :
Se desenharmos duas diagonais, de vértice a vértice, sem interseção, formam-se três triângulos isósceles. A soma da área desses triângulos é igual à área do pentágono.
Se unirmos cada vértice ao centro da figura geométrica, teremos 5 triângulos equiláteros restantes. Com a soma da superfície desses cinco triângulos também obteremos a superfície total.