A geometria é um ramo da matemática que se concentra no estudo das formas, tamanhos e propriedades de objetos geométricos, como pontos, retas, segmentos, polígonos e círculos.
Um dos tópicos fundamentais da geometria, e em particular dos triângulos, é o estudo de ângulos e segmentos, e um dos teoremas mais importantes relacionados a esses conceitos é o teorema da bissetriz.
Este teorema desempenha um papel crucial na divisão de ângulos e segmentos, e tem aplicações em diversas áreas da matemática e da física.
Definição de ângulos e bissetriz
Antes de mergulharmos no teorema da bissetriz, é importante compreender alguns conceitos-chave da geometria. Um ângulo é a região formada por dois raios que compartilham um ponto comum, denominado vértice. Os ângulos são medidos em graus e um ângulo completo equivale a 360 graus. Em muitos casos, precisamos dividir um ângulo em duas partes iguais, e isso nos leva à noção de bissetriz.
Uma bissetriz de ângulo é uma reta, semirreta ou segmento que divide o ângulo em dois ângulos congruentes, ou seja, dois ângulos que possuem a mesma medida. Em outras palavras, a bissetriz corta o ângulo pela metade. No caso de um ângulo de 90 graus, a bissetriz resultante teria um ângulo de 45 graus de cada lado.
O teorema da bissetriz do triângulo
O teorema da bissetriz afirma que, em um triângulo, a bissetriz de um ângulo divide o lado oposto em segmentos proporcionais aos outros dois lados. Pode parecer uma afirmação complexa, mas podemos decompô-la e compreendê-la melhor através de um exemplo.
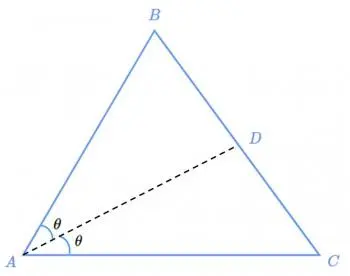
Considere um triângulo ABC, onde o ângulo no vértice A é dividido ao meio por uma linha que cruza o lado oposto BC no ponto D. O teorema nos diz que a razão entre BD e CD é igual à razão entre AB e AC.
Matematicamente, isso pode ser expresso da seguinte forma:
Este teorema é especialmente útil na resolução de problemas de geometria envolvendo ângulos e segmentos. Pode nos ajudar a encontrar comprimentos desconhecidos ou demonstrar propriedades de triângulos e outras figuras geométricas.
Prova do teorema da bissetriz
A prova do teorema da bissetriz envolve o uso de propriedades de triângulos semelhantes e a aplicação do teorema de Tales. Aqui está uma breve explicação de como isso é demonstrado:
-
Começamos com o triângulo ABC e sua bissetriz que cruza o lado BC no ponto D.
-
Aplicamos o Teorema de Tales, que afirma que se tivermos duas retas paralelas cortadas por retas transversais, são criados segmentos proporcionais. Neste caso, traçamos uma reta paralela aos lados AC e BD que passa pelo ponto C.
-
Isso nos dá dois triângulos semelhantes: ACD e ABC, onde os ângulos são iguais e as retas são paralelas, o que implica segmentos proporcionais.
-
Usando a propriedade de similaridade dos triângulos, podemos afirmar que:
Esta é a igualdade que queríamos provar e assim a prova do teorema está concluída.
Exemplos de aplicações do teorema
O teorema da bissetriz tem diversas aplicações em geometria e matemática. Alguns dos exemplos de aplicação mais comuns incluem:
- Resolução de problemas de geometria: O teorema é usado para encontrar comprimentos ou ângulos desconhecidos em triângulos e outras figuras geométricas quando certas relações de proporção são conhecidas.
- Demonstração das propriedades dos triângulos: Usado para mostrar que certos triângulos são semelhantes ou que certos pontos estão em linha reta.
- Construção Geométrica: Ajuda na construção de ângulos bissectados com precisão, o que é útil em diversas aplicações de design e arquitetura.
- Estudos de trigonometria: O teorema também é aplicado em trigonometria para resolver problemas relacionados a senos, cossenos e tangentes.
- Resolução de problemas de física: Usado em física para compreender as trajetórias das partículas e a direção das forças em sistemas físicos.
