O triângulo, figura geométrica composta por três segmentos que conectam três vértices diferentes não alinhados, representa uma das formas poligonais fundamentais da geometria. A sua relevância na ciência e na tecnologia remonta à antiguidade, visto que é uma das figuras geométricas mais essenciais e amplamente utilizadas.
Uma característica significativa dos triângulos é a sua invariabilidade, tornando-os elementos cruciais no projeto arquitetônico, como a Torre Eiffel, baseada em uma composição de formas triangulares, e na engenharia, incluindo estruturas fixas para painéis solares. Além disso, desempenham um papel fundamental na geometria, pois todos os polígonos podem ser decompostos em triângulos.
Características dos triângulos
Os triângulos são figuras geométricas fundamentais com diversas características que definem sua estrutura e propriedades. Aqui estão algumas das características mais importantes dos triângulos:
- Três lados : Triângulos são polígonos que possuem exatamente três lados. Esses lados são segmentos de linha que conectam três pontos chamados vértices.
- Três ângulos : Cada triângulo consiste em três ângulos internos em seus vértices.
- Soma dos ângulos : Em um triângulo, a soma dos ângulos internos é igual a 180 graus. Isto é válido para qualquer tipo de triângulo, seja equilátero, isósceles ou escaleno.
- Lados e ângulos correspondentes : Em um triângulo, os lados e ângulos correspondentes são iguais em triângulos congruentes. Congruência refere-se à igualdade de forma e tamanho.
- Altura e mediana : Em um triângulo, a altura é um segmento de reta perpendicular a um lado e que passa pelo vértice oposto. A mediana é um segmento que conecta um vértice ao ponto médio do lado oposto.
Tipos de triângulos
Estas figuras geométricas podem ser classificadas de acordo com diferentes critérios:
Devido ao tamanho dos ângulos internos pode ser:
- Triângulo agudo : todos os ângulos internos são agudos (menos de 90 graus).
- Triângulo obtuso : existe um ângulo maior que 90 graus.
- Triângulo retângulo : um dos ângulos mede 90 graus, um ângulo reto. Nesse caso, os dois lados que formam um ângulo reto são chamados de catetos e o lado oposto ao ângulo reto é chamado de hipotenusa.
Como na geometria euclidiana a soma dos ângulos de um triângulo é 180º. Portanto, pelo menos dois ângulos do triângulo devem ser agudos (menos de 90º).
Devido ao número de lados iguais, esses números podem ser:
- Triângulo escaleno : os três lados não são iguais.
- Triângulo isósceles s: dois lados são iguais. Esses lados são chamados de lado, o terceiro lado é chamado de base. Em um triângulo isósceles, os ângulos da base são iguais.
- Triângulo equilátero : todos os três lados são iguais. Em um triângulo equilátero, todos os ângulos são iguais a 60°.
Calcular a área e o perímetro de um triângulo
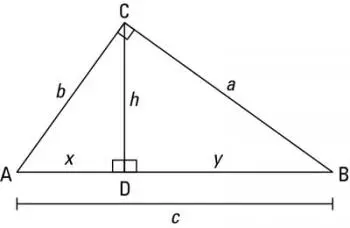
Com base na figura abaixo, para obter o perímetro e a área de um triângulo, podemos utilizar as seguintes fórmulas:
Perímetro
Para calcular o perímetro basta somar os comprimentos dos lados da figura: a + b + c.
Área
A fórmula para encontrar a área de um triângulo é metade do produto da base (não dos lados) pela altura:
A = (b h) / 2
Caso não saibamos a altura, podemos aplicar a fórmula de Heron.
Onde:
-
a, b e c correspondem aos três lados da figura geométrica.
-
A é a área
-
s é o semiperímetro (encontre o perímetro e divida por dois):
No caso de um triângulo retângulo, um dos catetos é a base e o outro corresponde à altura. Assim fica mais fácil calcular a área.
Propriedades e teoremas
Teorema de Pitágoras
O teorema de Pitágoras é um dos resultados geométricos mais famosos e úteis. Aplica-se a triângulos retângulos, aqueles com ângulo reto (90 graus). O teorema afirma que num triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos outros dois lados. Matematicamente, é expresso como:
a² + b² = c²
Onde “a” e “b” são os comprimentos dos catetos e “c” é o comprimento da hipotenusa.
O teorema de Pitágoras é fundamental em geometria e trigonometria e é aplicado a uma ampla variedade de problemas, desde o cálculo de distâncias em mapas até a resolução de equações quadráticas.
Teorema da Bissetriz
O teorema da bissetriz refere-se à bissetriz de um ângulo em um triângulo. Afirma que a bissetriz de um ângulo divide o lado oposto ao ângulo em dois segmentos que são proporcionais aos outros dois lados do triângulo. Matematicamente, é expresso como:
a/d = b/e
Onde "a" e "b" são os comprimentos dos lados do triângulo e "d" e "e" são os comprimentos dos segmentos em que a bissetriz divide o lado oposto.
Este teorema é útil para calcular segmentos em triângulos e encontrar pontos de intersecção em ângulos bissetores.
Teorema de Tales
O teorema de Tales é uma ferramenta poderosa para relacionar segmentos em triângulos semelhantes. Afirma que se uma reta paralela corta dois lados de um triângulo, ela divide esses lados em segmentos proporcionais. Matematicamente, é expresso como:
m/n = p/q
Onde "m" e "n" são os comprimentos dos segmentos de um lado do triângulo e "p" e "q" são os comprimentos dos segmentos correspondentes do outro lado.
O teorema de Tales é fundamental na resolução de problemas geométricos e na demonstração das propriedades de triângulos semelhantes.