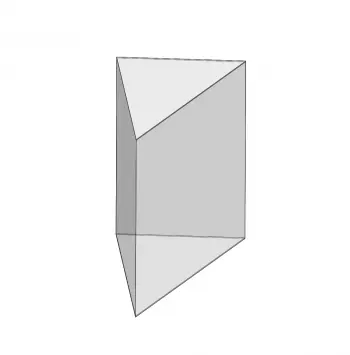
O termo "prisma triangular" refere-se a um sólido geométrico tridimensional que tem uma base triangular e faces laterais que são paralelogramos. Em outras palavras, é um prisma com uma base em forma de triângulo.
Um prisma triangular tem três faces retangulares e duas faces triangulares, tornando-o um prisma específico e distinto. As faces laterais são paralelogramos porque possuem lados opostos paralelos e congruentes.
A altura do prisma triangular é a distância entre as bases paralelas e pode variar em comprimento dependendo do tamanho e das proporções do prisma.
O prisma triangular é apenas uma das muitas formas de prismas existentes, e sua geometria específica lhe confere propriedades e características únicas. Pode ser utilizado em diversas aplicações, como arquitetura, geometria ou física, dependendo das necessidades e contextos específicos.
Volume de um prisma triangular: fórmula e cálculo
O cálculo do volume de um prisma triangular é feito multiplicando a área da base pela altura do prisma. Aqui estão os três passos para calculá-lo:
-
Calcule a área da base triangular: Para um triângulo, a área é calculada usando a fórmula da área do triângulo, que é (base x altura) / 2.
-
Determine a altura do prisma: A altura do prisma é a distância perpendicular entre as duas bases paralelas.
-
Multiplique a área da base pela altura.
Fórmula específica para o prisma triangular:
V = (b t h t / 2) h p
Onde:
-
V é o volume do campo geométrico.
-
b t é a base do triângulo a partir de uma de suas bases.
-
h t é a altura do triângulo a partir de uma de suas bases.
-
h p é a altura do prisma.
Área de um prisma triangular: fórmula e cálculo
Para calcular a área de um prisma triangular, é necessário conhecer as áreas da base e dos retângulos que formam as faces do poliedro. Quer dizer:
-
A área da base do triângulo: (base x altura) / 2
-
O perímetro da base do triângulo, que é a soma de seus três lados.
-
A altura do prisma.
Usando a fórmula da área do triângulo, a área da base pode ser calculada usando a seguinte fórmula
A = 2 A t + p t h
Onde,
-
A é a área do prisma triangular.
-
A t é a área da base do prisma.
-
p t é o perímetro da base triangular.
-
h é a altura do prisma.
Caracteristicas
As principais características de um prisma triangular são as seguintes:
-
Bases: O prisma triangular tem duas bases que são triângulos congruentes. Essas bases são paralelas entre si e estão localizadas em extremidades opostas do prisma.
-
Faces Laterais: O prisma triangular tem três faces laterais retangulares. Essas faces conectam as arestas das bases e formam paralelogramos.
-
Arestas: O prisma triangular possui nove arestas no total: três arestas que formam as bases triangulares e seis arestas que conectam os cantos das bases com os cantos das faces laterais.
-
Ângulos: As bases triangulares têm três ângulos e cada face lateral tem quatro ângulos retos (90 graus). Além disso, as faces laterais adjacentes fazem ângulos de 90 graus entre si.
-
Volume: O volume de um prisma triangular é calculado multiplicando a área da base pela altura do prisma. A área da base é obtida pela fórmula da área de um triângulo (base x altura / 2).
-
Área: A área total de um prisma triangular é obtida somando a área das duas bases triangulares e das três faces laterais retangulares.
-
Simetria: Um prisma triangular tem simetria em relação a um plano que passa pelo centro do prisma e é paralelo às bases triangulares.
Exemplos
Aqui estão alguns exemplos de objetos ou estruturas que podem ser representados como prismas triangulares:
-
Barracas: Algumas barracas possuem estrutura em forma de prisma triangular. As bases da tenda são geralmente triangulares e as faces laterais são retangulares.
-
Torres de sinalização: algumas torres de sinalização, como as utilizadas em telecomunicações ou sistemas de transmissão de sinal, podem ter formato de prisma triangular. As bases seriam os triângulos de sustentação e as faces laterais seriam os painéis retangulares que abrigam os equipamentos ou antenas.
-
Edifícios arquitetônicos: alguns edifícios modernos usam projetos arquitetônicos que incorporam prismas triangulares em sua estrutura. Esses prismas podem ser elementos ornamentais na fachada ou mesmo formas geométricas definidas na estrutura principal do edifício.
-
Piscinas: Algumas piscinas ao ar livre ou piscinas de formato incomum podem ter uma forma de prisma triangular. Nesse caso, as bases seriam as formas triangulares da piscina e as faces laterais seriam as paredes retangulares que circundam o perímetro.
-
Rampas de acesso: Às vezes, prismas triangulares são usados para criar uma rampa de acesso que permite que pessoas em cadeiras de rodas superem a elevação de um meio-fio.