No campo da geometria, os planos são elementos básicos e fundamentais. Definidos como superfícies planas infinitas que se estendem em todas as direções, os planos são elementos fundamentais que nos ajudam a compreender formas e estruturas em duas dimensões.
Neste artigo, explicaremos o que são planos na geometria, suas características distintivas e como são aplicados em diversos contextos matemáticos e práticos. Desde a concepção de figuras geométricas até à resolução de problemas e ao desenvolvimento de aplicações tecnológicas, os planos desempenham um papel vital na nossa compreensão do espaço e da forma.
O que é um plano?
Na geometria, um plano é uma superfície plana infinita que se estende em todas as direções.
Você pode pensar em uma folha de papel que se estende para sempre, sem ser grossa. Neste caso não há limites nem arestas, é como um mundo infinito em duas dimensões!
Características de um plano
As principais características que definem um plano no espaço são as seguintes:
- Infinito em todas as direções: Uma das características mais importantes é que ele se estende infinitamente em todas as direções. Isso significa que não importa o quão longe você se afaste de um ponto do plano, você sempre encontrará mais espaço.
- Sem espessura: Ao contrário dos objetos tridimensionais, como uma bola ou um cubo, um plano não tem espessura. Imagine que você está olhando um desenho em uma folha de papel. O desenho está no plano do papel, mas o papel é tão fino que podemos considerá-lo sem espessura.
- Representado por linhas: Em geometria, representamos planos por meio de linhas. Essas linhas podem ser retas ou curvas e se estenderem em todas as direções dentro do plano. Quando desenhamos figuras geométricas num plano, utilizamos estas linhas para mostrar como elas se relacionam entre si.
- Independente do sistema de coordenadas: Um plano é independente do sistema de coordenadas usado para representá-lo. Isto significa que independentemente de como os eixos x e y sejam escolhidos, as propriedades básicas do plano, como o seu infinito e a falta de espessura, permanecem inalteradas.
- Contém infinitos pontos: como se estende infinitamente, contém infinitos pontos. Cada ponto do plano é único e pode ser identificado pelas suas coordenadas, se for utilizado um sistema de coordenadas.
- Não determina uma direção preferencial: Ao contrário das linhas e segmentos, que possuem uma direção específica, o plano em si não possui uma direção preferencial. Pode ser considerada como uma superfície sem orientação em que as direções são igualmente válidas.
Tipos de planos
Na geometria, existem vários tipos de planos que são utilizados para diferentes fins e aplicações. Aqui estão alguns dos tipos mais comuns:
- Horizontal: Um plano horizontal é aquele que se estende horizontalmente em relação à superfície da Terra. Num sistema de coordenadas tridimensional, um plano horizontal não se inclina nem desvia verticalmente.
- Vertical: Ao contrário do anterior, um plano vertical se estende verticalmente e é perpendicular à superfície terrestre. A vertical é útil em geometria para representar relações espaciais no espaço tridimensional.
- Inclinado: Um plano inclinado é aquele que não é horizontal nem vertical, mas forma um ângulo em relação a ambos. As inclinações são comuns em problemas de física e mecânica, onde são usadas para estudar forças, inclinações e movimentos.
- Cartesiano: Este tipo é um sistema de coordenadas bidimensional que consiste em dois eixos perpendiculares, geralmente denominados x e y. É amplamente utilizado em matemática para representar pontos, gráficos e funções.
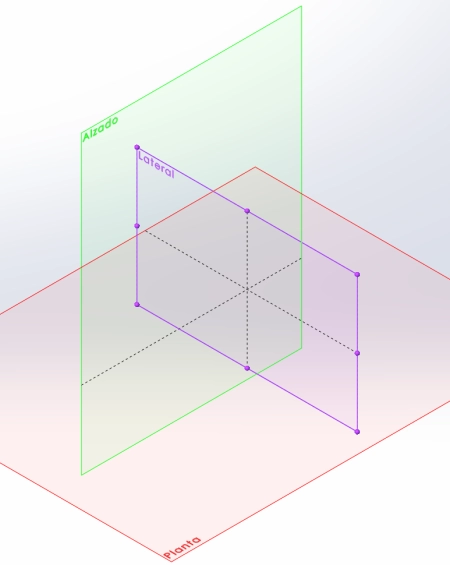
- Projeção: Em desenho técnico e design, um plano de projeção é usado para representar objetos tridimensionais em duas dimensões. Os planos de projeção incluem três planos: planta, elevação e lateral, que mostram diferentes vistas do objeto em diferentes ângulos.
- Tangente: Um plano tangente é aquele que toca uma superfície em um único ponto e é perpendicular à linha que passa por esse ponto. Os planos tangentes são importantes no cálculo e na geometria diferencial para representar a relação entre curvas e superfícies em um determinado ponto.
- Paralelo: Um plano paralelo é aquele que não se cruza com outro plano e mantém a mesma distância em todo o seu comprimento. Os planos paralelos são úteis em geometria para estudar propriedades de linhas e ângulos em relação a superfícies paralelas.
- Perpendicular: Um plano perpendicular é um tipo especial que forma um ângulo reto (90 graus) em relação a outro plano ou linha.
Diferença entre plano e área
Em geometria, o termo “plano” refere-se a uma superfície bidimensional que se estende infinitamente em todas as direções, como uma folha de papel. É uma entidade abstrata sem espessura, definida pela intersecção de duas linhas ou por sequências de pontos no espaço.
Por outro lado, “área” é uma medida quantitativa da extensão de uma superfície bidimensional. Representa a quantidade de espaço coberto por uma figura no plano e é expresso em unidades quadradas (como metros quadrados ou centímetros quadrados).
Embora um plano seja a própria superfície, a área é a medida numérica de quanto espaço essa superfície ocupa.