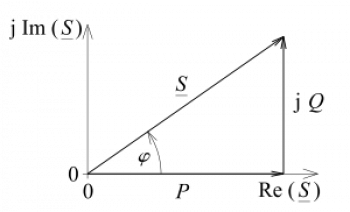
O triângulo de potência, também conhecido como triângulo de Watt, é uma representação gráfica usada na teoria elétrica para analisar a distribuição de potência em um circuito de corrente alternada (CA).
Baseia-se nas propriedades trigonométricas de um triângulo retângulo, o que nos permite calcular e compreender a relação entre as três potências fundamentais de um sistema elétrico:
- Potência aparente (\( S \)) : Representa a potência total fornecida ao circuito e é medida em volt-amperes (VA). É a combinação vetorial de potência ativa e reativa.
- Potência ativa (\( P \)) : É a potência útil que é transformada em trabalho real, como a iluminação ou o movimento de motores. É medido em watts (W).
- Potência reativa (\( Q \)) : É a potência que não realiza trabalho útil, mas é necessária para o funcionamento de equipamentos com elementos indutivos (como transformadores e motores). É medido em volt-ampères reativos (VAR).
Fórmula do triângulo de potência
O triângulo é formado por três lados, onde:
- A hipotenusa representa a potência aparente (\( S \)).
- A perna adjacente é a potência ativa (\( P \)), relacionada ao cosseno do ângulo de fase (\( \cos\theta \)).
- O cateto oposto é a potência reativa (\( Q \)), relacionada ao seno do ângulo de fase (\(\sin\theta \)).
- Matematicamente, a relação entre essas potências é expressa pelo teorema de Pitágoras:
\[ S^2 = P^2 + Q^2 \]
O fator de potência (FP) é definido como a relação entre potência ativa e potência aparente:
\[ FP = \cos\theta = \frac{P}{S} \]
Quando o fator de potência é baixo, significa que há uma alta proporção de potência reativa, o que reduz a eficiência do sistema elétrico.
Exemplos práticos do triângulo de potência
Abaixo mostramos três exemplos práticos
Motor elétrico com baixo fator de potência
Um motor de indução consome 10 kW de potência ativa e tem uma potência reativa de 6 kVAR devido à sua natureza indutiva.
A potência aparente será:
\[ S = \sqrt{(10^2 + 6^2)} = \sqrt{100 + 36} = \sqrt{136} \aprox 11,66 \text{ kVA} \]
Sistema de iluminação com correção do fator de potência
Um conjunto de lâmpadas LED consome 5 kW com potência reativa de 1 kVAR.
A potência aparente será:
\[ S = \sqrt{(5^2 + 1^2)} = \sqrt{25 + 1} = \sqrt{26} \aprox 5,1 \text{ kVA} \]
Transformador com carga indutiva
Um transformador fornece 50 kW a um sistema com uma carga indutiva que requer 30 kVAR.
A potência aparente do sistema será:
\[ S = \sqrt{(50^2 + 30^2)} = \sqrt{2500 + 900} = \sqrt{3400} \aprox 58,3 \text{ kVA} \]
Para que serve o triângulo de potência?
O triângulo de potência é uma ferramenta fundamental na análise e projeto de sistemas elétricos. Suas aplicações incluem:
Cálculo de potência elétrica
Permite determinar a distribuição de potência em um circuito:
- A potência aparente total (S) fornecida.
- Potência ativa (P), que é convertida em energia útil.
- Potência reativa (Q), que representa a energia trocada entre componentes indutivos e capacitivos.
Otimizando o desempenho do circuito
Ao compreender a distribuição de energia, as perdas de energia podem ser minimizadas e o fator de potência melhorado, reduzindo assim o consumo desnecessário de energia reativa e otimizando o uso da rede elétrica.
Projeto de sistemas elétricos
É utilizado para dimensionar equipamentos elétricos, garantindo que transformadores, geradores e cabos sejam adequados para suportar a potência necessária sem sobrecarga ou perdas excessivas.
Correção do fator de potência
Muitos sistemas elétricos industriais exigem bancos de capacitores para compensar a potência reativa e melhorar o fator de potência, reduzindo assim a demanda de energia da rede e diminuindo os custos operacionais.
Análise de falhas e manutenção preventiva
O triângulo de potência permite detectar problemas em sistemas elétricos, como perdas de energia por alta reatância ou desequilíbrios de carga, ajudando a prevenir falhas e otimizar a manutenção.
Exercício resolvido sobre o triângulo de potência
Enunciado:
Existe um circuito elétrico com potência aparente de 800 VA e fator de potência de 0,8. Calcule a potência ativa e a potência reativa do circuito.
Solução:
Primeiro, podemos calcular a potência ativa (P) do circuito usando a fórmula P = S x cos(θ), onde θ é o ângulo de fase entre a corrente e a tensão. Neste caso, como o fator de potência (FP) é igual a 0,8, sabemos que cos(θ) = FP = 0,8. Portanto, podemos calcular a potência ativa da seguinte forma:
\[
P = 800 \, VA \vezes 0,8 = 640 \, W
\]
A potência ativa do circuito é de 640 watts.
Então, podemos calcular a potência reativa (Q) do circuito usando a fórmula Q = S x sin(θ). Sabemos que o ângulo de fase (θ) pode ser calculado a partir do fator de potência usando a seguinte fórmula:
\[
\cos(\theta) = \text{FP} \quad \Rightarrow \quad \sin(\theta) = \sqrt{1 - \cos^2(\theta)}
\]
Neste caso, como FP = 0,8, podemos calcular sin(θ) da seguinte forma:
\[
\sin(\theta) = \sqrt{1 - 0,8^2} = \sqrt{1 - 0,64} = \sqrt{0,36} = 0,6
\]
Portanto, podemos calcular a potência reativa da seguinte forma:
\[
Q = 800 \, VA \vezes 0,6 = 480 \, VAR
\]
A potência reativa do circuito é de 480 volt-amperes reativos.
Portanto, a potência ativa do circuito é 640 W e a potência reativa é 480 VAR.