O teorema de Gauss para o campo elétrico afirma que o fluxo de um campo elétrico através de uma superfície fechada (superfície gaussiana) é dado pelo quociente entre a carga elétrica total dentro da superfície dividida pela constante dielétrica absoluta do meio (ε 0 ). Qualquer carga pontual externa à superfície não contribui de forma alguma para o fluxo total.
A equação gaussiana faz parte das quatro equações de Maxwell.
O campo elétrico produzido por dois objetos com carga estática pode ser obtido por dois procedimentos equivalentes: aplicando a lei de Coulomb ou usando a lei de Gauss. A lei de Coulomb é uma forma mais simples e direta de expressar a força elétrica. Por outro lado, a lei de Gauss é mais sutil, mais elegante e às vezes mais útil.
O teorema de Gauss tem uma utilidade muito prática. Em sua formulação física relativa aos campos elétricos, é traduzido em última análise em uma fórmula simples, utilizável por todos e com implicações práticas muito significativas.
O fluxo de cargas que cruzam a superfície gaussiana é proporcional ao número de linhas de campo que a cruzam.
Declaração do teorema de Gauss
Aqui está o enunciado do teorema de Gauss para o campo elétrico: o fluxo de um campo elétrico através de uma superfície fechada é dado pela relação entre a carga elétrica total dentro da superfície e a constante dielétrica absoluta do meio.
Fórmula da lei de Gauss
Olhando para a fórmula do teorema de Gauss para o campo elétrico, podemos escrever
A declaração gaussiana fornece uma maneira rápida e fácil de calcular o fluxo do campo elétrico através de uma superfície fechada. Simplesmente calcule a soma algébrica de todas as cargas que estão dentro da superfície e divida pela constante dielétrica absoluta.
É importante destacar alguns aspectos:
-
Se pensarmos no vácuo, podemos substituir a constante dielétrica absoluta do meio ε m pela constante dielétrica do vácuo cujo valor conhecemos.
-
Para calcular a soma algébrica de todas as cargas internas, é necessário levar em consideração os sinais das cargas, que podem ser positivas ou negativas.
-
A superfície pode ter qualquer formato, desde que esteja fechada.
-
O que importa é a carga total dentro da área de superfície. Se houver outras cargas localizadas fora da superfície, elas não devem ser consideradas para fins de cálculo de fluxo.
-
O teorema é válido para qualquer tipo de campo elétrico, não necessariamente uniforme no espaço. A fórmula também é válida para qualquer configuração de carga.
Exemplo da lei de Gauss
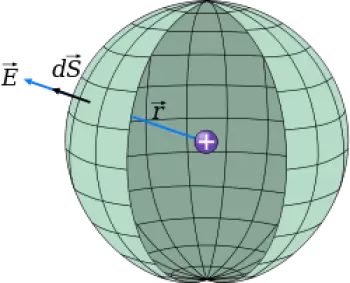
Suponha que desejemos calcular o campo elétrico produzido por uma carga pontual e usar a lei de Gauss para encontrá-lo.
Em nosso exemplo, vamos imaginar uma superfície esférica gaussiana de raio r com uma carga (q) contida em seu centro. Para calcular a integral de fluxo, assumiremos que, devido à simetria do problema, E deve ter a direção radial para fora da carga (q). Isso implica que E é paralelo a dS em todos os pontos da superfície de espera.
Também pela simetria devemos supor que E depende apenas da distância r da carga q ao ponto considerado, de forma que E terá o mesmo valor para qualquer ponto da esfera, e será constante na integração.
Nessas condições, o cálculo do fluxo através da superfície esférica será:
Φ = E (4 · π · r²)
Já que a integral é simplesmente a área da superfície da esfera. Uma vez que a carga total contida em nossa esfera é q, a lei de Gauss nos dá: